Fare un ricerca su Google per sapere cos’è un frattale, oppure consultare Wikipedia.
Si legge che un frattale è un oggetto geometrico che ripete la sua struttura allo stesso modo su scale diverse all’infinito, insomma non cambia aspetto anche se visto con una lente di ingrandimento. Sono esempi di frattali le foglie della felce e la forma del cavolfiore.
Non preoccupiamoci ora della natura dei frattali o dei frattali in natura e di tutta la matematica che è stata costruita attorno negli anni 70, ma facciamolo noi un frattale, per divertimento.
Ci serve un foglio grande su cui è disegnato un quadrato. Da questo quadrato ricaviamo tre copie ridotte del 50%. L’operazione può essere eseguita con una fotocopiatrice.
Ritagliamo i 3 quadrati e li incolliamo facendo combaciare coppie di lati. Ripetiamo la stessa operazione su ogni quadrato ottenuto ( lo riduciamo del 50%, ne facciamo tre copie e sostituiamo il quadrato grande con i nuovi tre).
Ripetere la stessa operazione, se continuiamo all’infinito otterremo un frattale.
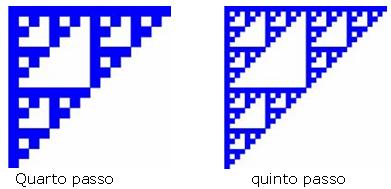
Ecco fatto un famoso frattale: la gerla di Sierpinsky. E’ stato facile vero?
L’operazione che è stata eseguita è analoga a quella che avviene in campo biologico, abbiamo agito come un codice genetico: immaginiamo una cellula madre che genera tre cellule figlie e ciascuna a sua volta genera tre cellule figlia e così via.
La natura produce molti esempi di forme molto simili ai frattali; è anche possibile notare fenomeni di auto-similiarità nella forma di una costa: con immagini riprese da un satellite man mano sempre più ingrandite si nota che la struttura particolare di golfi e insenature mostra molte componenti che rassomigliano molto alla forma complessiva su scala più grande. Mandelbrot cominciò a studiare i frattali proprio approfondendo altri studi sulle irregolarità delle coste inglesi, scoprendo tantissime affinità fra tali figure e molte forme del mondo reale. Oggi si ritiene universalmente che i frattali possano descrivere il mondo in maniera molto più precisa e accurata che non le vecchie figure piane euclidee, che sono solamente approssimazioni delle forme reali. Gli utilizzi attuali della geometria frattale sono i più disparati: alcuni economisti hanno sviluppato teorie che arrivano a prevedere le oscillazioni del mercato secondo modelli matematici frattali, mentre c’è sempre maggior interesse sulla componente artistica della geometria frattale: si organizzano annualmente varie competizioni in merito, nelle quali artisti con sufficienti cognizioni matematiche possono presentare le loro creazioni. Ecco alcuni esempi:
Ora un gioco solo per ragazzi.
A TRE A TRE
Prendi le prime tre parole e cerca quale lettera hanno in comune tutte e tre. Quando l’hai trovata, cancella il primo nome e cerca quale lettera hanno in comune le tre parole che si trovano ora in testa alla lista. Continua nello stesso modo finché non hai individuato anche la lettera comune alle ultime tre parole della lista. Leggendo una di seguito all’altra tutte le lettere che hai man mano trovato scoprirai il nome di un infaticabile marciatore greco.
CILINDRO
USCIRE
SCUOLA
QUATTRO
ATTESA
TERRENO
PRENDERE
PRATO
PASTICCIO
FISCHIARE
SEDUTO